ditjes en datjes

De Grote Vierkanten varieren in grootte van
30 x 30 cm tot 40 x 40 cm.

De stramienen verschillen soms in grootte
en fijmazigheid, maar natellen leert
dat bovenstaande afmetingen overeenkomen
met 100 kruissteekjes voor 30 cm breed en
140 kruissteekjes voor 40 cm breed
Dat houdt in dat ze pakweg tussen de
100 x 100 = 10.000 kruissteekjes en
140 x 140 = 19.600 kruissteekjes zijn.

Ik neem voor het gemak 15.000 kruissteekjes per Groot Vierkant als gemiddelde.

Dat betekent voor mij:  5 x 15.000 =  75.000
En voor mijn moeder:   19 x 15.000 = 285.000

Dat komt op een totaal van 75.000 + 285.000 = 360.000


Nog een rekensommetje:

1 strengetje splijtzij
is ongeveer 8 meter lang.
Dat knip ik in 8 draden, van 1 meter lang. 
Die halveer ik in dikte (van 6 naar 3 draadjes) 
Dus ik heb 8 x 2 = 16 draden

1 draad maakt gemiddeld 40 kruissteekjes.

1 streng splijtzij maakt dus 40 x 16 = 650 kruissteekjes.

Dat zou moeten betekenen dat 360.000 : 650 = 553,9 strengetjes splijtzij door mijn moeder en mij al zijn opgeborduurd.


-----------------------------------------------------------

Over de getallen van Fibonacci (Bron: Wikipedia)



De rij van Fibonacci is genoemd naar Leonardo van Pisa, bijgenaamd Fibonacci, die de rij noemt in zijn boek Liber abaci. In woorden is elk element van de rij steeds de som van de twee voorgaande elementen, beginnend met 0 en 1. De rij blijkt interessante eigenschappen en verbanden te bezitten met onder andere de gulden snede. De eerste elementen van de rij (rij A000045 in OEIS) zijn dan als volgt:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...
Het is evenwel niet duidelijk wie als eerste de rij heeft uitgedacht. Toen Fibonacci 20 jaar was, ging hij naar Algerije waar hij Indiase en Arabische wiskunde bestudeerde. Wellicht leerde hij daar de rij kennen.
Men laat de rij ook wel met 1 en 1 beginnen in plaats van 0 en 1.
De manier waarop de rij van Fibonacci gedefinieerd is, is een voorbeeld van wat in de wiskunde een recursieve definitie genoemd wordt. Dit betekent dat de elementen vastgelegd worden op basis van een of meer voorgaande elementen; dit leidt tot een differentievergelijking. Het 'ne getal van Fibonacci wordt zo gegeven door:
f_0 = 0\,
f_1 = 1\,
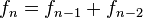f_n = f_{n-1} +f_{n-2}\, , voor n > 1
De eerste twee elementen zijn per definitie 0 en 1, soms ook 1 en 1 waardoor de eerste 0 wegvalt. Ook andere waarden voor de eerste twee elementen zijn mogelijk, maar leveren een andere rij (bijvoorbeeld de rij van Lucas).
Veel differentievergelijkingen hebben geen gesloten uitdrukking of expliciet voorschrift, waarmee het ne element enkel aan de hand van het getal n bepaald kan worden. Voor de rij van Fibonacci bestaat een dergelijke uitdrukking wel, namelijk:
f_n = \frac{(1+\sqrt 5)^n - (1-\sqrt 5)^n}{2^n \sqrt 5}
Bovenstaande formule, voor het het eerst gepubliceerd in 1730 door Abraham de Moivre, is op het eerste zicht opvallend omdat fn een geheel getal is, terwijl de formule wortels bevat. Zie differentievergelijking voor een bewijs van deze formule.

Voortbrengende functie

Uit de recursievergelijking kan worden afgeleid dat de voortbrengende functie voor de rij van Fibonacci gelijk is aan:
\sum_{n=0}^\infty f_n x^n = \frac{x}{1-x-x^2}.
Dit kan op volgende manier:
S = \sum_{n=0}^\infty f_n x^n = f_0 x^0 + f_1 x^1 + \sum_{n=2}^\infty f_n x^n.
= 0 + 1 x + \sum_{n=2}^\infty (f_{n-2} + f_{n-1})x^n.
= x + x^2 \sum_{n=2}^\infty f_{n-2} x^{n-2} + x \sum_{n=2}^\infty f_{n-1} x^{n-1}.
= x + x^2 \sum_{n=0}^\infty f_n x^n + x \sum_{n=1}^\infty f_n x^n.
= x + x^2 \sum_{n=0}^\infty f_n x^n + x (-f_0 x^0 + (f_0 x^0 + \sum_{n=1}^\infty f_n x^n)).
= x + x^2 S + x ( \sum_{n=0}^\infty f_n x^n).
= x + x^2 S + x \ S.
S = \frac{x}{1 - x - x^2}.

 Heel leerzaam toch?
-----------------------------------------------------------










1 opmerking:

  1. Ineke20 december 2010 om 18:18

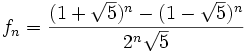
    jaja, die Fibonacci kan me wat. Maar het ziet er professioneel uit! Leuk. Het is wel verslavend Dit wordt hard doorborduren om het iedere keer een beetje actueler t emaken. Dan heb ik het een stuk makkelijk met truien enzo.

    BeantwoordenVerwijderen

Abonneren op: Posts (Atom)